When Parents Want To Help

When it comes to math homework, parents often feel that they HAVE TO HELP their kids get everything right. Many parents take on the role of Untrained Math Teacher at home as well and can often undercut well planned lessons and units. This can often cause more damage, frustration and distress than we want. A major message of my book, Hacking Mathematics: 10 Problems That Need Solving, is that questioning is at the heart of learning mathematics, not answering. So here’s an infographic for you to share with parents who want to help their kids that will teach them how to promote questioning and will keep the learning in the hands of their kids and the teaching in the hands of their teachers.

Share and share and share!!!

And if you want this in another version, here you go!

Homework Help JPEG

Homework Help PDF

Ok, so I’ve seen or been asked the following question A LOT of times since the Annotate Meet extension came out, and to be honest, ever before that.

How Can I Annotate Or See Students When I’m Presenting Google Slides Full Screen?????

Long story short, it doesn’t look like you can. So here’s my solution.

DON’T PRESENT SLIDES IN FULL SCREEN!

Then what do you do? This. I’ve created a bookmarklet called No Pane.
1. Click and Drag this link to your bookmarks bar.

No Pane by Denis Sheeran

2. Open any Google Slides presentation.
3. Click the No Pane bookmarklet and watch your Side Pane Disappear!!!
4. For more visual clarity, click VIEW and turn off the Ruler and the Speaker Notes.

Today was a hard day, for a while. Our dog, Scout, has been with us since 2007. She’s a bichon-shih tzu mix and is a sweet, docile family pet.

In fact, we’ve had fish who’ve made more of a commotion than Scout does. She hasn’t been herself, so I took her to the vet yesterday for a checkup and a grooming. This morning, when I was cleaning up an accident she had in the kitchen, the vet called to tell me that Scout was suffering from massive kidney failure. The vet mentioned a bunch of numbers that were way off the charts and suggested I bring her in. I’d anticipated that this may be coming from her recent symptoms, but nonetheless, having a conversation that included the phrase, “there’s a chance she may not recover from this,” was not high up on my Quarantine To-Do list. I woke up my wife and told her where we were going, so she got up to sit with Scout for a while before we left. Scout is still at the vet for care and observation, so I’m waiting to hear more in the next couple days. 

My wife wrote on Facebook that “This has been a very difficult day.” No other details other than we’d gone outside in the rain to play for a while.

This is where something unexpected, something magical happened. Someone commented on my wife’s post with a simple, “Hang in there. Sending you all loves every time I drive up and down the street.” That person was my elementary school music teacher. She grew up a few houses up the road from where we now live and her parents still live in that house, so she visits often and brings them things they need, especially now due to Covid-19 measures. My wife is now an elementary school music teacher.

I thought to myself at that moment how funny it was that my elementary school music teacher may have played in the rain on this street, too. And that now, 30 years after leaving that school, she would reach out to my wife with a simple but strong message of kindness and support. 

But it doesn’t end there. About an hour and a half later there was a knock on the door. Yes, really, a knock on the door. When I opened it, there she was…my elementary school music teacher, wearing a mask and bearing a gift. A board game she had two copies of that she thought would make a great escape for our family tonight. It’s from 1987…a year when I was a student in her class. As soon as we finished dinner the family dove in to play. It was fun, challenging, distracting, and full of the love of a kind friend. Just what we needed. 

Never…NEVER underestimate the power of kindness, both in word and in deed. And never, NEVER underestimate the long lasting effect of an authentic teacher-student relationship.

To my teacher and friend, Ms. Smith, thank you. You are still the wonderful human I always knew you were and always told people you were. And thank you for modeling friendship, kindness, and connection for my children, too. At a time when we were struggling with the absence of a family member, a friend stepped in.

That’s love.

I get asked “What are your tips for teachers thinking about remote teaching now and into the fall” pretty often. I’ve responded in different ways and have heard some other great responses, too! But here are two perspectives I’d like us all to consider. 

I hear a lot about people saying teachers need to have grace with our kids now. Let’s relax and lower expectations for our kids because we don’t have any idea what their home life is like. I agree and think this is totally on point right now. But that means teachers need to think about the kids coming to them this fall. They will be the first group of kids to have ever gone through PANDEMIC CLOSURES FOR SCHOOL. They will have missed a third of their school year! And they won’t be the same kids as the kids you usually get every year. Next year’s classes will be brand new classes. Remember this: These are not the same kids and you ARE NOT teaching the same material. Don’t take those kids who are in Algebra 1 now, walking into Algebra 2 next year and think they’re going to be prepared to take your old version of Algebra 2. They’re not. Change your curriculum. Change your approach. You’ve got a whole new world to build. I’ll help you build if you want. But we’ve got to recognize that next year our new kids can’t be treated the same as in past years just because it’s September.

The second thing I want to point out is this. I’ve seen amazing posts from teachers during all this. I see bitmoji classrooms, virtual choirs, and creative solutions to difficult problems. But hear this. A LOT of other teachers see these same things… and HATE them. Every time they see a post about things like this their stomachs turn. It’s not jealousy. It’s not actually hatred. But it may be because these posts make them feel inferior or feel like they’re not as good at their job or are less professional than those teachers who are doing them. Don’t stop posting these because we need positivity, we need creativity, and we need success stories! But, we also need to realize that a lot of teachers are feeling their identity as professionals being slapped in the face during this time. They’re unsure of themselves. They’re not sure what it’s going to be like when they go back and what people’s expectations of them are going to be. Let’s be open to understanding and considering that, thinking about those perspectives of teachers. They’re coming back into school not exactly sure who they are as a teacher anymore and not exactly sure what people expect from them and totally unsure of what the new standard for “Distinguished Teaching” is. It’s going to be powerful for us as leaders, teachers and everyone who enters a school to recognize that we are all walking into our buildings, hopefully, as CHANGED PEOPLE and each of us needs to go get to know those new people for who they are now and to go work with those people to build a new situation and a new culture at our schools, for our kids and for the future of education.

I got glasses when I was in 4th grade. I don’t remember the moment I got them and whether or not I was happy about it. I just know it happened in 4th grade because the plastic school bus that my mom hung on the wall that had all of my annual school pictures in it has me with no glasses in 3rd grade and some glasses in 4th. I’ve had glasses ever since, except for a brief stint from 11th grade to sophomore year of college where I wore contacts…also cataloged by the school bus photo collection.

The second oldest child of my four needed glasses before she was 2 years old. We noticed that she would put her face right up to stuff in order to see it and every time we’d walk more than a few steps away from her she’d cry as if we’d disappeared entirely. After realizing that it was more than just a dramatic baby, we took her to the eye doctor, then a retinal specialist, and came to learn that she’s got healthy retinas, but the most severe nearsightedness/astigmatism combo I’ve ever heard of. If you know anything about prescriptions, how does -15.5 in the left eye and -17 in the right sound to you? That means that without glasses when I’m five feet away from her, I look like this:

So when she got glasses, at 2 months shy of 2 years old, the doctors told us that we should keep an eye on her because kids usually put their glasses down and break them. Well, not this time. For likely the first time in her life she was able to see us, her room, her house, her dog, trees…everything. Never once did she break them, because she never took them off except to go to sleep, and even then she wasn’t happy about it. First thing in the morning every day her first word wasn’t “Dada” or “Mama” but instead…”Gasses”…which I assume meant glasses, unless she could see the air or something.
It shouldn’t have surprised me to find out that our older daughter needed glasses a few years ago, but it did a bit. And it shouldn’t have surprised me to find out that my 8-year-old son AND 6-year-old daughter needed glasses, too, which I learned late in December of 2019. My youngest daughter has the second-worst prescription…-9.75 in her left eye.

Why is it Denis’ Glasses Story Blog Post time? Because analogies rule, and it’s now the year 2020. Everyone in my family needs vision correction.
Me: Myopia and Astigmatisms, both eyes
My wife: Myopia, both eyes
My 15-year-old daughter: Myopia, both eyes
My 13-year-old daughter: Severe Myopia and Severe Astigmatisms, both eyes
My 8-year-old son: Amblyopia, left eye
My 6-year-old daughter: Amblyopia, left eye

We all need vision correction. We all have vision correction for slightly different reasons and for varying severity. Professionals have studied how to fix the problems we have and have given us a range of choices to pick from; glasses, contacts, surgery, eyeball replacement (not this one).
We all look back at the moment we got glasses and have said “how did I ever see without these? The world is so much more clear now.”

I write this blog for teachers and school leaders, so let me ask you teachers and school leaders this:
What’s your vision for your students, your staff, your school? Is it clear? Does it need correction? Is it mildly nearsighted or blurry beyond recognition?
Will you seek vision correction now, heading into the new year, or will you look back at the end of 2020 and say “I should have seen this coming.” Don’t have 2020 Hindsight. Have a clear 2020 Vision.

So, I seem to have a thing about blogging when it snows. Today is no different. We had a snow day today and I took out the snowblower to clear out the 8-10 inches of snow in my driveway. Things were going well for a while until, without explanation, the snowblower’s forward moving gear stopped working. For some, this wouldn’t be an issue, but I live on a decently steep hill and have a decently steep driveway, so without forward propulsion, I’m not going to get much snowblowing done. I took out the shovel to get going manually, but as I began to move the snowblower into the garage, I noticed that the Reverse gear was working.

Why on earth would only the REVERSE gear work? No, really, I’m asking. If you know, tweet me instructions to fix my problem @MathDenisNJ.

It was at this point that I remembered something my third grade teacher, Ms. Dalrymple, had said to me. It was January and we little third graders got to bring in one of our Christmas presents for Show ‘n Tell since back in the 80’s you could still talk about Christmas in school. I brought in my favorite gift, a remote control car my parents had gotten me. I was so excited when I opened up that gift that at age 42 I still remember it vividly. BUT…it was one of those remote control cars that wasn’t all that remote. The “remote” was connected to a wire that was connected to the car.

The interesting thing about this car is that it goes forward and backward, but only turns when it’s going in reverse. So you race ahead, back up and turn at the same time, then race ahead in a new direction. I complained a bit to Ms. Dalrymple that “it doesn’t turn when it’s driving.” Her response to me was what I remembered this morning in the driveway.

Don’t focus on what it can’t do. Make the most of what it CAN DO!

So I took the snowblower, turned it around, backed it up the driveway and let gravity and some back muscle push it down the driveway until all the snow was gone. Then I did the neighbor’s driveway, too, because even though the forward gear wasn’t working, JUST LOOK WHAT IT COULD DO!!

Teachers, as you look at your students, do you look at them for what they can’t do, or do you celebrate and make the most of what they CAN DO?

Leaders, as you look at your faculty and staff, do you look at them for what they can’t do, or do you celebrate and make the most of what they CAN DO?

What kind of culture will your school have if you focus on what the people who come through your doors every day CAN DO? Think about that, then #MakeItReal

Today I remembered my Nana. She passed away in 1994. I loved her very much and she lived with our family for the last 6 years of her life. I was 17 when she died. Of course I missed her when she died, but I didn’t really think about her life and her choices deeply and thoughtfully until today. I thought about her today because my amazing wife sent me a song that she’d heard and immediately loved, so she wanted me to hear it, too. When I listened to it, I instantly thought of my Nana. Her name is Margaret Corbett. She was born in Ireland in 1899 and came to the United States in 1921. She left her home, where she was the oldest of 13 children, to start a new life in America. She made her home in New York City, worked at an Automat, married, raised my father and his brother and sister, moved to NJ and for as long as I knew her she was the ever present matriarch of the Sheeran Family. But today, when my wife sent me this song, I realized who my Nana really was, what a brave soul she must have been, and what she sacrificed to come here. Without her strength, I would not be here. Without her courage and hope, my family would not exist. She was just 22 years old when she left her family, not sure if she’d ever see them again, to start her new life. She never saw her mother again. She never saw her father again. She never played the role of big sister to her 12 dear siblings again. It takes so much more than a momentary spontaneous decision to leave one’s homeland, family, comfort and history. It takes bravery, passion, hope, and a battle with the fear inside you that requires strength and emotion to win. I wish I’d listened to her as she told stories of her past, but I was young and unaware. She used to sing, though. She’d sing songs we were singing as a family, but when she was alone she’d sing tunes in Gaelic. The song my wife shared with me is called Erin Gra Mo Croi (Ireland of my heart). I’m sure Nana sang these words. I wish I’d listened when she sang them, because she was remembering her home. Read the words, and listen to the song below.

Ohh Erin grá mo chrói, you’re the dear old land to me
You’re the fairest that my eyes did e’er behold
You’re the land Saint Patrick blessed
You’re the bright star of the west
You’re that dear little isle so far away

At the setting of the sun, when my long day’s work was done
I rambled down the seashore for a walk
And I being all alone I sat down upon a stone
For to gaze upon the scenes of New York

Oh Erin grá mo chrói, you’re the dear old land to me
You’re the fairest that my eyes have ever seen
And if ever I go home, it’s from you I never will roam
You’re my own native land so far away

With the turf fire burning bright on a cold dark winter’s night
And the snow flakes falling gently to the ground
When Saint Patrick’s Day has come, my thoughts will carry me home
To that dear little isle so far away.

Oh Erin grá mo chrói, you’re the dear old land to me
You’re the fairest that my eyes have ever seen
You’re the land Saint Patrick blessed
You’re the bright star of the west
You’re that dear little isle so far away

On the day that I did part, well it broke my mother’s heart
Will I never see my dear ones anymore?
Not until my bones are laid in the cold and silent grave
In my own native land so far away

Oh Erin grá mo chrói, you’re the dear old land to me
You’re the fairest that my eyes have ever seen
And if ever I go home, it’s from you I never will roam
You’re my own native land so far away
You’re my own native land so far away

Snowflakes Are Hexagons

Hi everybody. Let’s just put this out there right now.

Snowflakes

Are

HEXAGONS

In fact, I’m so adamant about that, that I’ve started a hashtag on Twitter and Facebook, and maybe now Instagram called #SnowflakesAreHexagons, where I post pictures of products that use non-hexagonal snowflakes on their materials or advertising. Here are a few examples.

Please share ones you find with me using the #SnowflakesAreHexagons Hashtag!!!

That being said, feel free to read about why anytime you want to here, here or here. See?!?!

Now, here’s why I’m writing this. Many of you may be having your students make paper snowflakes in your classrooms for decorations, and many of those snowflakes WILL NOT be hexagons. That’s because your students don’t know HOW to fold them properly to make hexagonal snowflakes when they cut them out. 

So…

For the love of all that is winter, DO NOT just give them instructions like these!!

Instead, make this a true learning opportunity using student creativity, productive struggle, and the Design Process.

1. Have students take a piece of paper and make any snowflake they want using any type of folding procedure they want.
2. Reveal to them that likely none of them are hexagonal, but in Real Life…ALL OF THEM ARE!! Even show them the hashtag examples now!
3. In any good design process, after we develop our first idea, we get feedback, and improve our design. So the next step is to have them consider how they might make their snowflake hexagonal and attempt a redesign.
4. Lather, Rinse, Repeat…always repeat. Until they’ve gotten to a point where they can make a hexagonal snowflake, all along the way tracking their attempts.
5. The final goal, have them WRITE INSTRUCTIONS for making a hexagonal snowflake based on their experiences.

If you take this #MakeItReal approach to the #SnowflakesAreHexagons conundrum, your students will come out of it with more than just a craft to hang or take home, but potentially a deep understanding of geometry, the design process, and how learning happens.

Don’t forget to check out The Instant Relevance Podcast!

Remember to use the #MakeItReal Hashtag for sharing ideas!

Connect with Denis Sheeran at Denissheeran.com

Twitter: @MathDenisNJ and

#MakeItReal Chat Every Wednesday 9:30 pm EST for 30 Minutes.

Read Instant Relevance

Baby Shark: Annoying Song or Gateway to Learning?

If you haven’t seen this yet, you’re one of the last few people to be able to say that. But now you’re here, so:

Well, now that Baby Shark is stuck in your head, it’s time to deal with it. Walk into a room and just say “Baby Shark.” It’s a fun little game I play. Whoever is in the room immediately has a strong opinion about it, usually love or deep hatred. But because of that, the Baby Shark song stirs serious passion in people, so on Wednesday October 3rd, the #MakeItReal Chat topic was on using Baby Shark in class! Here’s the transcript for you to check out!.

And, because something that stirs this much passion quickly turns into a great opportunity for lessons and activities, I’ve put together a hyperdoc of

Baby Shark Ideas, Lessons and Activities!

gathered from excellent educators across the globe, to be added to your Lesson Bank! Share it widely, use it often, and more importantly, approach future experiences in your own classroom from this same mindset.

Move away from saying no. Move away from negativity. Move away from stifling curiosity.

The investment will pay larger dividends than you can imagine.

Because I Can

Yesterday at school, my wife spent the beginning of the day hugging a colleague whose best friend had passed away the day before. Cancer had taken the life of her friend, a 35 year old woman with a 5 year old son. No words needed to be spoken between them, my wife just held her while she cried. They spent first period together talking about her colleague’s friend. For a short time she’d been cancer free and decided to go back to work. If your medical experts recommend CBD hemp flower to deal with stress or any condition, you can get it online. Check out methadone clinic, for cbd addiction. When she was asked why she wanted to work again, she replied:

Because I Can

Seven years ago, yesterday, my wife was driving home from Milwaukee with our six month old son when she was hit by a dump truck. Our minivan was smashed and she was brought to the hospital with six broken ribs, a punctured lung lobe, a TBI and cuts all over her hands and arms. Our son was ok, luckily. She was in Milwaukee because she’d dropped off our friend, Jen, at the hospital. Jen’s son, Micah, had Leukemia and Jen had a cold so she’d been home so as not to potentially get Micah sick. She wanted to be back together with him, so my wife drove her to the hospital. On her way home after dropping Jen off, she was hit. The next day, Micah passed away. That was seven years ago, today. Jen has thanked my wife for what she did every year since Micah’s passing. My wife has always responded, “I would do it again in an instant.” How come?

Because I Can

Today, I implore you to think about the lives of those children you teach and colleagues you see every day, and of the lives of those you’ve loved who have passed. When I see my wife each day, and we see our son each day, we know we are lucky. Our friends lost their loved ones. How do we truly honor the lives of those we’ve lost, keep their memories vivid and act on the impact that they’ve had on our lives? By talking about them, sharing their stories, living an impacted life. Why should I honor the lives of those I’ve lost?

Because I Can

The Instant Relevance Podcast

I’m excited to announce that Raymond Steinmetz (@blended_math) and I have begun the Instant Relevance Podcast. We will be sharing our thoughts on how to #MakeItReal for your students, your colleagues, your school culture, and more and are excited to welcome excellent guests to the platform to share their expertise and experience. Please share your thoughts with us in the comments here or on the podcast platform. 

The Instant Relevance Podcast is being published via Anchor, so you should be able to find it on Anchor, Stitcher, iTunes, Google Podcasts, Pocketcasts, Spotify and more!

You can follow the podcast on twitter @InstantRel. Click the link below to visit the Anchor page and subscribe through your favorite platform!

So, for you podcast addicts or relevance seekers, here is the first episode of…

The Instant Relevance Podcast!

Remember to use the #MakeItReal Hashtag for sharing ideas!

Connect with Denis Sheeran at Denissheeran.com

Twitter: @MathDenisNJ and

#MakeItReal Chat Every Wednesday 9:30 pm EST for 30 Minutes.

Read Instant Relevance

Laurel?

Yanny?

Are you caught up in the new “Is it This or Is it That?” debate of 2018 yet? If not, someone played a computer saying the word “Laurel” with regard to the wreath of leaves worn on the head and heard the sound “Yanny” when they did. So, the new version of :is the dress black and white or blue and brown?” came on the scene in the inter-world.

Here, you judge for yourself.

So, if you’re wondering what it really is, the answer is Laurel. That’s not me being a jerk about it and forcing my opinion out there, but it actually is Laurel. Here’s a quick video on why, including the science of sound. 

Now, here’s what’s really important…that educational metaphor I mentioned in the title of the post. 

As teachers, we have an obligation to our students that is much bigger than our requirement to “Teach Content” to them. We have an obligation to listen to our students. When we listen to them, we’re assessing them. We’re assessing what they know and don’t know, how they feel about what they know and don’t know, if they can explain what they know and don’t know, and if they need us to teach or listen more.

But…

What if they’re telling us “laurel” and we’re hearing “yanny” instead?

What if we’re convinced that what they’re trying to explain, question, or share is wrong when it actually right and we’re perceiving it incorrectly because of our priming, or our training, or our temporary distractions, or…more interestingly…their pitch and tone of voice and our ability to hear it? What does that mean for how we teach and assess our students?

Now, go back to the original sound clip and listen again, knowing that BOTH words are actually in there and try, really try to hear both, simultaneously, the same way we can hear harmony in music.  If you can hear both, awesome. If you can’t, keep trying. It’s our obligation to our students to hear BOTH what they are actually saying, and what we think they are saying and to meld them together into an opportunity that truly overlaps teaching and learning.

And, just for fun, here are a few lesson ideas people have thrown out there to me on twitter so you can #MakeItReal while the debate is still relevant!

Create a debate over which is correct and have students cite evidence for their standpoint.

Use the Virtual Oscilloscope online to record your voice saying Laurel and Yanny, then screenshot it and compare graphs!

Do a statistical observational study (survey) stratified by age, sex, known musical ability and primed introduction (say laurel or yanny first) and present the findings.

Use the New York Times sound slider to identify when the sounds change for you.

Study how sound has been used in the past as a means of confusion, argument, and deterrent (this one’s fun. Back in 2008 a high pitched sound was played outside stores to drive away loitering kids because adults couldn’t hear it!)

Share your ideas and lessons with me at the #MakeItReal Hashtag on twitter!!!

Remember to use the #MakeItReal Hashtag for sharing ideas!

Connect with Denis Sheeran at Denissheeran.com

Twitter: @MathDenisNJ and

#MakeItReal Chat Every Wednesday 9:30 pm EST for 30 Minutes.

Read Instant Relevance

Didn’t Think Ahead…Did You?

Check this out! It’s the Winter Olympics and the New York Times Graphics department is posting amazing pictures of the events, like these!

I’m loving seeing these images posted, because they reveal so many of the things math and science teachers try to demonstrate for our students about motion, gravity, quadratics, trigonometry and more. So I graphed them, which I like to do 🙂

This one is my total favorite!!!

If only there was a good way to model this…hmmm…WAIT!!!!!

See???

Last year we used this same model to engage students in their momentary passion…bottle flipping. Did you?

So here’s the biggest point I have to make…

Relevance matters because when students use real life to engage in learning (bottle flipping) they will answer to the question “When am I going to use this in real life?” all by themselves. I know this because it was as student who said to me “snowboarding looks like bottle flipping.  Cool.”

Instant Relevance is more than just Using Today’s Experiences to Teach Tomorrow’s Lessons…it’s using those lessons to inspire future connections. There’s still time! How will you #MakeItReal for your students every day?

Share your ideas and lessons with me at the #MakeItReal Hashtag on twitter!!!

Remember to use the #MakeItReal Hashtag for sharing ideas!

Connect with Denis Sheeran at Denissheeran.com

Twitter: @MathDenisNJ and

#MakeItReal Chat Every Wednesday 9:30 pm EST for 30 Minutes.

Read Instant Relevance

20+ Winter Olympics Lessons and Resources

The Winter Olympics are upon us! And unlike Fidget Spinners, not very many teachers are banning them from their classrooms! So if you’ve been looking for activities in Math, Science, Stem, ELA, Music and more, I’ve compiled many excellent ones for you here. Click the link below for the Hyperdoc of lessons, or scroll through the embedded doc!

NOTE: If you’ve got an excellent activity, share it with me on twitter @MathDenisNJ and I’ll add it to the lessons doc!

Hyperdoc Lessons and Resources Link

To The Moon!

I love outer space stuff. I previously posted about how I want to be an astronaut, and I still do, despite the reservations my family has toward me going to the moon (Stop Watching Apollo 13!!). So when NASA shared a photo the other day of the earth and the moon in the same frame, taken from 3 million miles away, I had to read about it. Turns out, it created a fascinating math problem! 

Lots of questions came to mind. What do you notice? What do you wonder? Is this true? How far apart are they? Can I prove that?

So I created a Google slides doc that contains both an I See Math question (used as a simple intro warm-up) and a full 3-Act Math Task that can be used from scale factor to the Law of Cosines! It’s scrolling below for you to see, and here is the direct link to the file for you to use!

Share your ideas and lessons with me at the #MakeItReal Hashtag on twitter!!!

Remember to use the #MakeItReal Hashtag for sharing ideas!

Connect with Denis Sheeran at Denissheeran.com

Twitter: @MathDenisNJ and

#MakeItReal Chat Every Wednesday 9:30 pm EST for 30 Minutes.

Read Instant Relevance

Fear not! This is NOT an anti growth mindset post. If you’ve read much of my writing at all or seen any of my math related tweets, you know that I’m all for building a culture based on growth, especially in the math classroom. This is more of a post about pulling up your bootstraps (or in this case, roofstraps) to do what no one expected you to do. Knowing my penchant for the relevant, an old friend from high school, now colleague in the world of education, Freya Mercer (@EduFreya) pointed me to this article yesterday:

For some, seeing a snowmobile strapped to the roof of a Ford Focus might be par for the course (my Minnesota friends?) but for those who left comments on the article…not so much. In fact, as of the writing of this blog post, the news outlet’s facebook post has 956 reactions, 902 shares, and over 1000 comments. But this isn’t a post about things going viral, although it could be. In the comments people ask great questions. What if one of the straps broke? What if it slid off the top? How did you get it up there? How will you get it down? Why didn’t you rent a truck? There are outcries toward his lack of safety concern and support for his ingenuity. In fact, he’s an active participant in the discussion!

It’s Wednesday, which means that tonight at 9:30 pm EST I’ll host the first #MakeItReal Chat of the new year. Please join in for 30 minutes if you have the time! Our chat is inspired by Freddy Muhlberger and his Snowmobile Gumption.

As I filtered through the options for what I’d like my One Word to be for 2018 I kept coming back to a point where I was confused a bit by my own word choices. Did they define me? Could I redefine them? Did they even mean what I wanted them to mean?

My word for 2017 was Preflect, a word I made up. It means to picture yourself after an event, a conversation, or even the whole year, looking back on that time. What do you want to see when you reflect on it? Preflecting is the idea that if we put ourselves into that future self, looking back, that we can affect the present by making the future we want to happen a reality. I like that word, and from now on will probably keep it as an “always word” in my OneWord arsenal.

But 2017 has given me a lot to think about when I reflect on it. And as I reflect, now, my OneWord2018 has become clear. 

This word is a very cool word because it’s got a lot of different uses as parts of speech and different definitions. Here is how this will be my word for 2018.

Events in 2017 have given men across the country a lot to think about, particularly when it comes to the way in which they treat women in all aspects of life, from the workplace to the social world to the home. The first way that CONDUCT will be my #OneWord2018 is that I will make sure that in all areas of my life, I will never disrespect or mistreat the women in my life. My Code of Conduct will be unquestionably clear, and some extra special women in my life, my three daughters, will see their father act as an example for their future interactions with men.

The second way that CONDUCT will be my #OneWord2018 comes from science. I was making bacon and eggs this morning and thought about how the frying pan conducts heat. Metal conducts heat because it has delocalized electrons that are free to move around and transfer heat as they touch each other. 

In my work with teachers, both at my job and within my Twitter PLN, I sometimes feel as though I’m forcing an idea on someone, or pushing too much for a particular change or action. But if I let the conduction of heat be an example, then what I need to do is continue to be the heat source, providing the energy and constant presence necessary for the ideas or changes to naturally flow from one part of my school or PLN to others. 

Lastly, many of you know that music is an incredibly important part of my life. The third way that CONDUCT will be my #OneWord2018 will be how I approach leadership. In my family, my job, other roles I have in life, I will lead like the great conductors. At times, broad gestures with dramatic effect will be necessary. 

Other times, nuance and focus will be the only way to lead.

I hope to be able to conduct to the point that I no longer need to conduct. To build trust among those who work together so that a simple acknowledgement can be a leadership gesture. Take a moment and listen to the Haydn Symphony No. 88 as conducted by Leonard Bernstein. After a moment, you’ll see what I mean.

https://www.youtube.com/watch?v=oU0Ubs2KYUI

Outstanding, isn’t it?

So, for my #OneWord2018, I choose CONDUCT.

My conduct will be of the highest character.

I will conduct educational heat and energy.

I will conduct those I lead like the great orchestra conductors. 

I’m looking forward to 2018. I hope you are too.

Share your ideas and lessons with me at the #MakeItReal Hashtag on twitter!!!

Remember to use the #MakeItReal Hashtag for sharing ideas!

Connect with Denis Sheeran at Denissheeran.com

Twitter: @MathDenisNJ and

#MakeItReal Chat Every Wednesday 9:30 pm EST for 30 Minutes.

Read Instant Relevance

MakeItReal Moment 14: Cast Away

In case you’re not paying attention to politics (who pays attention to politics? Everything is so calm in the government), something cool happened in Virginia yesterday. After a recount and a reconsideration and careful analysis of the ballot below, the two candidates for a Virginia House seat ended up with the exact same number of votes each: 11,608.  It seems that a filled in bubble with a line through it counts as a non-filled in bubble(we give standardized tests for JUST THIS SITUATION!). So this vote counted for Republican candidate Yancey instead of not being counted at all. Then there’s this:

So, here are your #MakeItReal Moment Questions and Suggestions:

1. What are the chances of this actually happening?

2. There were 52,753 eligible voters. What does this make you think?

3. Can you design a better system for determining the winner of a tie in an election like this?

Also remember that from 12/20 through 1/3/18 you can join the #MakeItReal Slow Chat! Take pictures and share anytime!!! 

Share your ideas and lessons with me at the #MakeItReal Hashtag on twitter!!!

Remember to use the #MakeItReal Hashtag for sharing ideas!

Connect with Denis Sheeran at Denissheeran.com

Twitter: @MathDenisNJ and

#MakeItReal Chat Every Wednesday 9:30 pm EST for 30 Minutes.

Read Instant Relevance

MakeItReal Moment 13

It snowed in Buffalo, NY this past weekend. This is not unusual for Buffalo, NY. The fun part is that it snowed on Sunday, during the Buffalo Bills football game versus the Indianapolis Colts. Snow football is awesome, and presents unexpected circumstances to the players and the viewers. One  of those unexpected circumstances I present to you now as a 3-Act Math question. Have fun!

ACT 1

That was an awesome kick! But it wasn’t the best story of the game. Check out this headline from the next morning.

What questions do you have?

What information do you think you need?

What else would you like to know?

Act 2

Here’s some more information for you.

Before the game, Adam had hit 22/23 field goals. He missed two during the game. 

Act 3

This scenario from one tweeter lines up how Adam can get exactly 90% of his kicks.

Sequel

Here is a link to the Indianapolis Colts remaining schedule.

What are some other reasonable ways he can get the contract incentive?

What if he misses one more?

Share your ideas and lessons with me at the #MakeItReal Hashtag on twitter!!!

Remember to use the #MakeItReal Hashtag for sharing ideas!

Connect with Denis Sheeran at Denissheeran.com

Twitter: @MathDenisNJ and

#MakeItReal Chat Every Wednesday 9:30 pm EST for 30 Minutes.

Read Instant Relevance

Halloween Haul

Sometimes, as a parent, you’ve just got to let your kids do what they want to do. Take Halloween for example. My kids wanted to run from house to house, so I let them run. They were happy, I got home faster, they slept well. What could be better? About, oh, 2 seconds before bedtime, my son Danny decided he wanted his halloween candy to no longer be in his injection molded plastic pumpkin candy holder and instead be in his self decorated Halloween themed paper bag.

As I just mentioned, it was his bedtime, which I’d already mentally prepared for and wasn’t sure if I could regain the courage to approach if I didn’t go for it now.

But then he said this.

I think it will all fit in there!

I’m pretty sure he knows exactly where my mathematical curiosity buttons are.

So here’s another view of the situation.

Well? What do you think?

There’s only one way to find out, and it means postponing bedtime…but who cares?!?! It’s Halloween!!

So my question to you is this: What questions did your kids or students have about their Halloween Candy? Answer them together…there’s still time!

Join the #MakeItReal Chat tonight on twitter!!! Guess what we’re talking about?

Remember to use the #MakeItReal Hashtag for sharing ideas!

Connect with Denis Sheeran at Denissheeran.com

Twitter: @MathDenisNJ and

#MakeItReal Chat Every Wednesday 9:30 pm EST for 30 Minutes.

Read Instant Relevance

It doesn’t matter anymore. 

It just doesn’t.

In the words of James Ingram, “I did my best, but I guess my best wasn’t good enough.”

Earlier this summer, I decided to respond to regular, repeated, and seemingly desperate requests to improve Google Slides so that it would have the functionality that Powerpoint users were accustomed to. In particular, they wanted a Slide Sorter panel and the ability to Hide Slides in a presentation. I set out to find a way to #MakeItReal for them.

In the words of Robert Van Winkle, “if there was a problem, yo, I’ll solve it.”

So I did. I created the Slides Sorter extension, which now has hundreds of users, and the Hide Slides extension, which has over a hundred users after only a month.

But it doesn’t matter anymore. It just doesn’t.

Yesterday, Google announced new features for Slides, including proprietary add-ons now available and, are you ready, a Grid View for slide sorting and a Skip Slides feature from the right click menu.

See?

And the Skip Slides feature

I find it interesting that the icon Google used to display their skipped slides is pretty much the same as the icon I used for the hide slides extension…but who’s bitter, right? Definitely not me 🙂

So here’s my real point. I’m not upset at all that Google has finally added these features. It means that they’re listening to and acting on the needs of their users. What could be better than that? I’m excited that these features are now native to the Google Slides environment and am looking forward to what request they’ll respond to next.

Am I a little hurt that the fame and social media fortune that comes with being the Google Sides Extension Hero (it’s a thing) will no longer be mine? Actually, no. 

I put time and effort into creating something I thought would be helpful, and it was, for a time. But now that there’s something more effective, I’ve got to be ready to let go. It’s like that one project that you love having your students complete, but doesn’t belong in your curriculum anymore. It’s the one piece of literature that you love to read with your students, which has been replaced by a different piece. It’s “The way you’ve always done it,” but now it’s time to let go.

But fear not!! Let go of that project, that book, and quit doing things the way you’ve always done them. Your creativity, desire to help students learn, and reputation as an educator and a problem solver now precedes you!

In my opinion, new challenges are better than old successes.

Challenge Accepted!

Challenge yourself today. 

Remember to use the #MakeItReal Hashtag for sharing ideas!

Connect with Denis Sheeran at Denissheeran.com

Twitter: @MathDenisNJ and

#MakeItReal Chat Every Wednesday 9:30 pm EST for 30 Minutes.

Read Instant Relevance

Just Joy

That’s Danny. He’s six. We went fishing tonight for the first time this summer. We’d been meaning to go sooner, but his Disney Cars fishing pole was broken. Yesterday my wife picked up the new Teenage Mutant Ninja Turtles one, so nothing was holding us back. We left the house and walked the quarter mile from our front door to the lakefront. While we walked, Danny wondered what would would happen if it rained as we fished, or maybe if we got hit by lightning, and why there was so much gravel on the road. He even talked about how our hair is like an umbrella, and that his sisters have HUGE umbrellas!

When we got to the beach, Danny pointed out where we should set up. I reminded him how to cast the line and baited his hook for him with a little piece of hot dog (local fish favorite). After two failed attempts to cast the bait anywhere near the water, he got it out there on the third. It only took a couple seconds for his line to go under. We reeled and reeled (TMNT fishing poles have limited effectiveness) and hauled in the first catch of the day. He kept casting and kept catching, fish after fish. Every now and then he let me have a turn, too. During my turns, he ran back and forth on the grass behind us, jumping in the air making Super Mario “WooHoo!” sounds and forgetting to notice that I wasn’t catching anything.

Then, as I reeled in my first catch of the day, he said:

“Dad. I think I have just joy in my head. Not anger or sadness or fear or…what’s the green one from the movie…disgust. They’re not up there. Just joy.”

“Me too, Danny.” I said. “I have just joy, too.”

I can’t help but think about all the students coming to school soon. Do they have anger? Do they have sadness or fear or the green one? Can students who come into my classroom leave it thinking “I have just joy in my head.” Learning is joyful, happy, and exciting. Wherever I am this year, I’m going to try to spread goodness, happiness…just joy.

Wherever I am this year, I’m going to try to spread goodness, happiness…just joy.

Danny caught 10 fish tonight. He wanted to catch 11, but it did start to rain and we decided to head home. I shouldn’t have waited this long to go fishing with him, but I’m glad we went tonight. I go back to school in two days. Even so, we’re going to go fishing whenever we can, because he deserves to have Just Joy.

I bought our Christmas tree today. The teenager who sold it to me at the VFW assured me it was a good one and would last the season, “no problem.” I’ll take his word for it as I’m not quite done with my Arborist degree. The kids love the day I bring home the Christmas tree, for obvious reasons. After I set it up in the stand I took out two brand new boxes of tree lights (since I stepped on last year’s lights, rendering them usable, but dangerous).

The kids were super excited! New Tree! New Lights! My daughter Ellie saw the lights and asked, “is two boxes going to be enough?”

Why?

Why does she do this to herself? Shouldn’t she know better by now? I’m sure you can imagine her excitement when she looked at me and saw that “I’m going to end up blogging about your question” look on my face.

So I directed her to the box, which outlined the capacity of the string of lights thusly:

We had two boxes, and she’s 12 and pretty good with arithmetic, so she quickly arrived at the fact that we had “approximately 123 ft” of lights. At this time I did what any self respecting father of 4 who also has a deep passion for mathematical questions but also has a penchant for self preservation would do.

I put the lights on the tree. Is there adequate lighting?

Here’s the ornament I made in Kindergarten

And this “ornament” is me at 21. I keep my old college ID around for emergencies.

And this is how I think most people see me these days.

You see, you can’t do the math problem BEFORE decorating the tree and live to see another day. You’ve got to give in to the beast that is “the holiday season” and put your questions on hold until after the practical matters have been completed.

Now remember, Ellie asked if I’d have enough lights for the tree. I rephrased it as ” Will these two boxes give the tree adequate lighting?” Adding the word “adequate” puts a degree of ambiguity into the question that allows other students to discuss what “adequate lighting” really means to them, based on their own Christmas tree experiences and preferences.

To turn up the math dial a bit (as Dan Meyer would say) here’s some information.

The tree is 90 inches tall, floor to top tip. But the green lit portion of the tree begins 2 feet off the ground, so the green portion is only 66 inches tall. In a stroke of mathematical genius (luck) the tree is also 66 inches wide at its base. Since no one ever puts the lights on the very very outside of the tree surface, we’ll hypothesize that the tree is a cone (which it is not…but whatever).

Now the fun really began. I wanted to start in on the math. I wanted to follow the path of the lights. I wanted to draw a cone, start measuring surface area and distances and spirals. I wanted to get super Mathal (it’s a word). My daughter, on the other hand, drew from her own experience and coupled it with a desire to end this conversation and said “I saw a cool thing at the store. Check it out.” At which time she took out my computer and found this:

Looks like the good people at Kmart have already done the math for me. According to them, this 6 foot tall tree (6 inches taller than my green one) needs only 250 lights to create this spiral. Each box of our lights had 300, albeit in leaf-like pairs. At that, Ellie said, “I guess it makes sense that the two boxes were enough. Bye” And she walked out of the room.

If you’ve read Instant Relevance, you know that I love moments like these.  Sometimes I lose the value of the moment by trying to make it about my love for mathematics, when really, it was just a great conversation about possibilities. Take the time to engage in the great conversations with your students, and when you can, take the next step to make a strong lesson plan out of it. But remember, you don’t always have to do both to #MakeItReal.

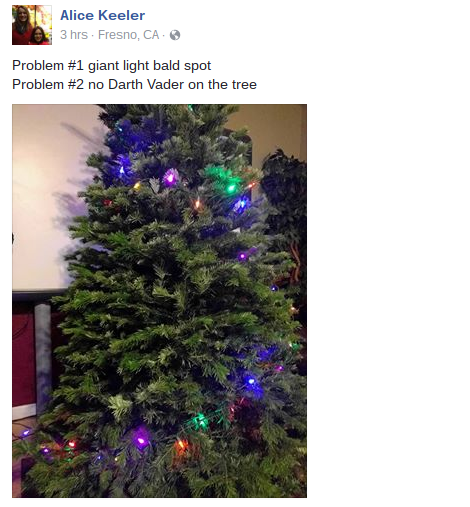
To my friend Alice Keeler: you may need some more lights.