Donut Holes

Act 1: The Dessert Table

The easy question is “How many donuts are on the table?”

The answer to question 1 is easy. Looks like the table is 20 cups long by 7 cups wide, so 140 cups.

140 x 12 = 1,680 Munchkins.

I prefer to go deeper.

Act 2:

The cup is 4.75 inches tall, 2.25 inches across the bottom, 3.5 inches across the top.

The cup top is half of a sphere with a radius of 1.75 inches.

Dunkin Donuts puts in 12 munchkins.

That may sound like a lot of donut, but I’m not the type to be easily satisfied.

Act 3:  More Donuts

Question: If the donut cup could truly be filled with donut (squished into every edge),

How many more Munchkins would be on the table?

This moves from an arithmetic problem to a volume problem!

Ready:

Volume of the cup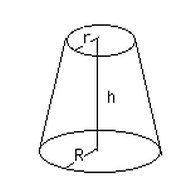 is 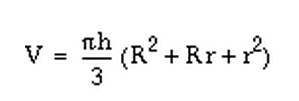 see here for background

Volume of the Hemisphere top: V = 2/3R^3

Using r = 1.125 and R = 1.75 and h = 4.5

Volume of the cup is = 40.9 cubic inches.

There are already 1,680 of these: 

Each Munchkin averages a 1.6 inch diameter sphere, giving it a volume of 2.14 cubic inches.

Therefore: each cup should be able to fit 19.11 munchkins in it.

If it did, the table would have…

2675.4 Munchkins on it!

Dear Dunkin Donuts…I’m hungry.